We now analyze an example of calculation the one-dimensional heat flow, (in an only direction, the edges are hypothetically isolated) to static regime through the layer of the termal interface material.
The thermal interface material is composed from a material, a thickness D, and from the surfaces S1 and S2 of peer area. The surface S1 is characterized by a temperature T1, while on the surface S2, T2 is the measured temperature. The quantity of heat expressed in watt (W) that it crosses the layer of the interface material it is calculated by the following equation:
Q = (lamda/d) * S (T1S-T2S)
Where lambda represents the thermal conductivity of the thermal interface material. Greater it is the thermal conductivity more heat passes. D is the thickness of the interface material measured in meters, and finally S is the measured area in meters at square, for some two equal surfaces S1 and S2. Thermal conductivity is expressed in W/meters x degrees Kelvin.
The thermal resistance is calculated by the following equation:
R = d / lambda
Where d is the thickness of the thermal interface material, and lambda is the thermal conductivity of the same one. As a rule, so much greater it will be the thermal resistance, so smaller will be the flow of transmitted heat. The thermal resistance is expressed in meters at square x degrees Kelvin/W. The figure 2 can help you in to understand the mechanism of calculations the one-dimensional heat flow.
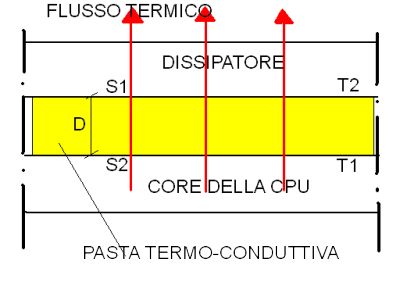
FIGURE 2.
(The mechanism of the conduction of the heat).
We have understood thing they mean the terms thermal resistance and thermal conductivity of a material, and we can now appraise with safety the thermal characteristics of a good interface material. But before progress we have to know of what the thermal interface material is made.
Menu Section/Preceding Page/Following Page/Returns to the Homepage.